Álgebra booleana Aviônicos ANAC (Portas Lógicas)
Este tópico é de grande relevância para o exame teórico da ANAC, e a compreensão aprofundada dos conceitos aqui apresentados será um diferencial na sua jornada.
Abordaremos as portas lógicas básicas, as portas universais, e técnicas para interpretar tabelas verdade, essenciais para a resolução de problemas práticos.
Portas Lógicas Básicas
As portas lógicas são os blocos construtivos fundamentais de qualquer circuito digital.
Elas realizam operações lógicas básicas com uma ou mais entradas binárias (0 ou 1) e produzem uma única saída binária. Vamos explorar as portas lógicas básicas:
Porta AND (E)
A porta AND, também conhecida como porta ‘E’, realiza a função de multiplicação lógica.
Sua saída é 1 (verdadeiro) somente se todas as suas entradas forem 1. Caso contrário, a saída é 0 (falso).
Função Matemática: A saída (S) de uma porta AND com entradas A e B é dada por: S = A * B ou S = A AND B .
Tabela Verdade da Porta AND:
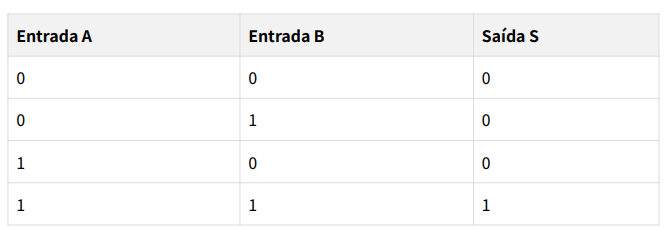
Como podemos observar na tabela verdade, a saída da porta AND é 1 apenas quando
ambas as entradas A e B são 1. Qualquer outra combinação de entradas resulta em uma
saída 0.
Porta OR (OU)
A porta OR, ou porta ‘OU’, realiza a função de soma lógica. Sua saída é 1 (verdadeiro) se
pelo menos uma de suas entradas for 1. A saída é 0 (falso) somente se todas as suas
entradas forem 0.
Função Matemática: A saída (S) de uma porta OR com entradas A e B é dada por:
S = A + B ou S = A OR B
Tabela Verdade da Porta OR:
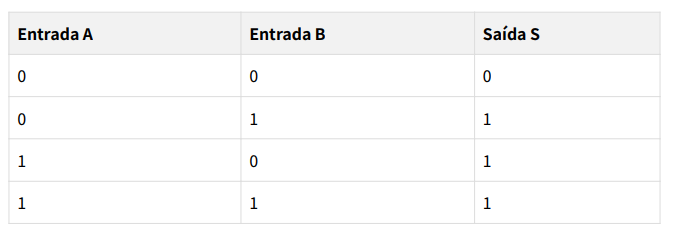
Nesta tabela, a saída da porta OR é 0 apenas quando ambas as entradas A e B são 0. Se
qualquer uma das entradas for 1, a saída será 1.
Porta NOT (NÃO)
A porta NOT, também conhecida como inversor, é a mais simples das portas lógicas, pois
possui apenas uma entrada e uma saída. Ela realiza a função de negação ou inversão
lógica. Se a entrada for 1, a saída é 0, e se a entrada for 0, a saída é 1.
Função Matemática: A saída (S) de uma porta NOT com entrada A é dada por: S = A’
ou S = NOT A (onde A’ representa a negação de A).
Tabela Verdade da Porta NOT:

Portas Lógicas Universais: A Porta NAND
Além das portas lógicas básicas, existem as portas lógicas universais, que são capazes
de implementar qualquer outra função lógica. As portas NAND (NOT-AND) e NOR (NOTOR) são exemplos de portas universais. Nesta aula, focaremos na porta NAND.
Porta NAND (NÃO-E)
A porta NAND é uma combinação da porta AND seguida por uma porta NOT. Ela realiza a
multiplicação lógica e, em seguida, inverte o resultado. Sua saída é 0 (falso) somente se
todas as suas entradas forem 1. Caso contrário, a saída é 1 (verdadeiro).
Função Matemática: A saída (S) de uma porta NAND com entradas A e B é dada por:
S = (A * B)\’ ou S = NOT (A AND B) .
Tabela Verdade da Porta NAND:
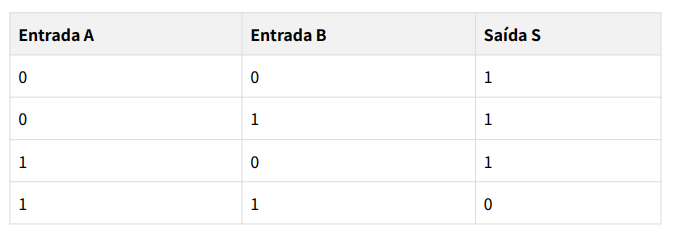
AND. Isso ocorre devido à inversão realizada pela porta NOT.
Derivando a Função Lógica a Partir da Tabela Verdade
Uma habilidade crucial na Álgebra Booleana é a capacidade de derivar a função lógica
de uma porta ou circuito a partir de sua tabela verdade. Isso é particularmente útil em
exames teóricos, onde você pode ser apresentado a uma tabela e precisar identificar a
porta lógica correspondente.
Regra do ‘1’ (para a porta AND)
Para portas como a AND, onde a saída é ‘1’ em apenas uma ou poucas combinações de
entrada, a estratégia é focar nessas linhas onde a saída é ‘1’.
Exemplo (Porta AND):
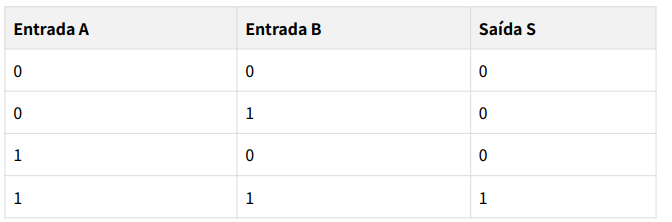
Neste caso, a saída é ‘1’ somente quando A é ‘1’ E B é ‘1’. Isso nos leva diretamente à
função S = A * B (A AND B).
Regra do ‘0’ (para a porta OR)
Para portas como a OR, onde a saída é ‘0’ em apenas uma ou poucas combinações de
entrada, a estratégia é focar nessas linhas onde a saída é ‘0’.
Exemplo (Porta OR):
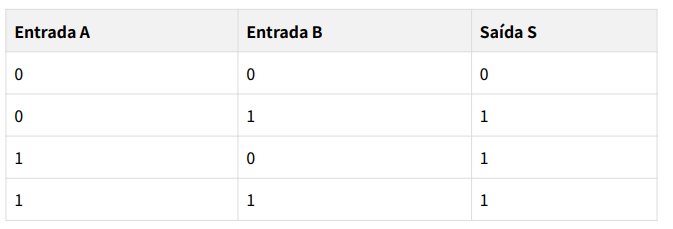
Neste caso, a saída é ‘0’ somente quando A é ‘0’ E B é ‘0’. Se aplicarmos as Leis de De Morgan (que veremos a seguir), podemos inverter essa lógica para encontrar a função OR. A ideia é que, se a saída é ‘0’ apenas quando A e B são ‘0’, então a negação dessa condição (A ou B) resultará em ‘1’.
Leis de De Morgan
As Leis de De Morgan são teoremas fundamentais na Álgebra Booleana que fornecem um método para converter expressões booleanas de uma forma para outra, especialmente útil na simplificação de circuitos lógicos. Elas estabelecem uma relação entre as operações AND, OR e NOT.
Existem duas leis principais de De Morgan:
Primeira Lei de De Morgan:
A negação de uma conjunção (AND) é equivalente à disjunção (OR) das negações. Em outras palavras, NOT (A AND B) é o mesmo que (NOT A) OR (NOT B) .
Matematicamente:
(A * B)\’ = A\’ + B\’
Segunda Lei de De Morgan:
A negação de uma disjunção (OR) é equivalente à conjunção (AND) das negações. Ou seja, NOT (A OR B) é o mesmo que (NOT A) AND (NOT B) .
Matematicamente:
(A + B)\’ = A\’ * B\’
Essas leis são poderosas ferramentas para a manipulação e simplificação de expressões lógicas, permitindo que os engenheiros convertam circuitos complexos em formas mais simples e eficientes.
Conclusão
Nesta aula, exploramos os conceitos fundamentais da Álgebra Booleana e das portas lógicas, essenciais para qualquer profissional da área de aviónica. Compreendemos o funcionamento das portas AND, OR e NOT, que são os pilares de todos os circuitos digitais.
Além disso, vimos a importância da porta NAND como uma porta universal e aprendemos técnicas para interpretar tabelas verdade e derivar funções lógicas.
As Leis de De Morgan, por sua vez, nos fornecem ferramentas valiosas para a manipulação e simplificação de expressões booleanas, otimizando o design de sistemas digitais. O domínio desses conceitos não apenas o preparará para o exame da ANAC, mas também o capacitará a entender e solucionar problemas em sistemas eletrónicos complexos a bordo de aeronaves.
GLOSSÁRIO – Álgebra Booleana e Portas Lógicas
Álgebra Booleana
Ramo da matemática que trabalha com valores binários (0 e 1) e operações lógicas. É a base para entender como circuitos digitais tomam decisões.
Conjunção (AND)
Operação lógica que só resulta em 1 quando todas as entradas são 1. Em linguagem simples: é um “E” rigoroso.
Derivação de Função a partir da Tabela-Verdade
Técnica para descobrir qual expressão ou porta lógica gera as saídas mostradas em uma tabela-verdade. Observa-se onde a saída é 1 (ou 0) para montar a função.
Disjunção (OR)
Operação lógica que resulta em 1 quando pelo menos uma das entradas é 1. Em linguagem simples: é um “OU” inclusivo.
Entrada Binária
Valor que entra em uma porta lógica, podendo ser 0 (falso) ou 1 (verdadeiro).
Inversor
Outro nome para a porta NOT. Inverte o sinal: se entra 1, sai 0; se entra 0, sai 1.
Leis de De Morgan
Regras que permitem transformar AND em OR (e vice-versa) quando se aplica a negação. Ajudam a simplificar e reescrever expressões lógicas de forma equivalente.
Multiplicação Lógica
Nome matemático para a operação AND. Usa-se “*” para representar a conjunção (ex.: S = A * B).
Negação (NOT)
Operação que inverte um valor lógico: 1 vira 0 e 0 vira 1.
Porta AND (E)
Bloco lógico que só gera saída 1 se todas as entradas forem 1. É associada à multiplicação lógica (S = A * B).
Porta Lógica
Elemento básico de circuitos digitais que realiza uma operação lógica (AND, OR, NOT, etc.) sobre sinais binários.
Porta NAND (NÃO-E)
Combinação de AND seguida de NOT. Só produz 0 quando todas as entradas são 1; em qualquer outro caso, a saída é 1. É considerada uma porta “universal”.
Porta NOT (NÃO)
Porta com uma única entrada que inverte o valor: entrada 1 vira saída 0 e vice-versa.
Porta OR (OU)
Porta que produz 1 quando pelo menos uma entrada for 1. Só produz 0 quando todas as entradas são 0. Corresponde à soma lógica (S = A + B).
Portas Universais
Portas que podem implementar qualquer função lógica apenas com sua combinação. NAND (e também NOR) são exemplos de portas universais.
Saída Binária
Resultado produzido por uma porta lógica após processar as entradas. Também é 0 ou 1.
Soma Lógica
Nome matemático para a operação OR. Usa-se “+” para representar a disjunção (ex.: S = A + B).
Tabela-Verdade
Quadro que lista todas as combinações possíveis de entradas e a respectiva saída de uma porta ou expressão lógica. Essencial para análise e projeto de circuitos.
Regra do “1” (para AND)
Ao analisar uma tabela-verdade de comportamentos do tipo AND, foque nas linhas onde a saída é 1; elas indicam diretamente a conjunção necessária (E simultâneo das entradas).
Regra do “0” (para OR)
Ao analisar uma tabela-verdade de comportamentos do tipo OR, foque nas linhas onde a saída é 0; com as Leis de De Morgan, é possível reescrever a expressão de forma equivalente e identificar a disjunção.
FAQ – Perguntas Frequentes
P: Como identifico rapidamente se uma tabela-verdade representa uma AND, OR ou NOT?
R: Observe o padrão da saída. Se só é 1 quando todas as entradas são 1, é AND. Se é 1 quando qualquer entrada é 1, é OR. Se há apenas uma entrada e a saída é sempre o oposto da entrada, é NOT.
P: Por que a porta NAND é chamada de “universal”?
R: Porque, combinando apenas portas NAND, é possível construir qualquer outra porta (AND, OR, NOT) e qualquer circuito lógico. Isso torna a NAND suficiente para implementar sistemas digitais completos.
P: Quando devo aplicar as Leis de De Morgan?
R: Use-as ao precisar transformar uma expressão com negação “por fora” (como NOT(A AND B)) em uma forma equivalente com negações “por dentro” (NOT A OR NOT B), facilitando a simplificação e a implementação do circuito.
P: Qual a diferença prática entre conjunção (AND) e disjunção (OR)?
R: AND requer que todas as condições sejam verdadeiras para gerar saída 1. OR exige que pelo menos uma condição seja verdadeira para gerar saída 1. Em termos de projeto, AND é mais restritiva; OR é mais permissiva.
P: Como usar a Regra do “1” e a Regra do “0” ao derivar a função?
R: Para padrões tipo AND, destaque as linhas com saída 1 e monte a expressão exigindo simultaneidade dessas condições. Para padrões tipo OR, destaque as linhas com saída 0 e, usando De Morgan, reescreva a expressão até revelar a estrutura OR.
P: O que significa “multiplicação” e “soma” lógicas no contexto das portas?
R: “Multiplicação” lógica corresponde ao AND (usar “*”). “Soma” lógica corresponde ao OR (usar “+”). São analogias matemáticas que ajudam a escrever e manipular expressões booleanas.
P: Em provas, é melhor memorizar símbolos ou entender o comportamento?
R: Entender o comportamento é mais eficiente. Saber “quando a saída é 1” para cada porta permite reconhecer rapidamente a função a partir da tabela-verdade e resolver questões com segurança.