Operações Aritméticas de Números Binários – ANAC AVIÔNICOS

Você já parou para pensar como os computadores realizam cálculos complexos em uma fração de segundo? A resposta está no coração da computação: o sistema binário. Diferente do nosso sistema decimal (base 10), o sistema binário (base 2) utiliza apenas dois dígitos: 0 e 1.

Essa simplicidade é a chave para a eficiência dos dispositivos eletrônicos, que representam informações através de estados de ligado (1) e desligado (0).

Seguindo o padrão da ANAC, Neste post vamos focar nas operações aritméticas fundamentais com números binários: soma, multiplicação e divisão, além de entender como converter números octais para binários.

Por Que o Binário é Tão Importante?

Os computadores e sistemas digitais operam internamente com o sistema binário. Cada “bit” (dígito binário) representa um estado elétrico, tornando o processamento de informações extremamente rápido e confiável. Entender como as operações aritméticas funcionam nesse sistema é fundamental para qualquer pessoa que queira compreender a lógica por trás da tecnologia.

1. Soma Binária: O “Vai Um” Digital

A soma binária é surpreendentemente similar à soma decimal, mas com um conjunto de regras mais simples, já que só temos 0 e 1. A operação é realizada bit a bit, da direita para a esquerda, considerando o “vai um” (carry) para a próxima coluna.

Regras Básicas:

• 0 + 0 = 0
• 0 + 1 = 1
• 1 + 0 = 1
• 1 + 1 = 10 (resulta em 0 e “vai 1” para a próxima posição)
• 1 + 1 + 1 = 11 (resulta em 1 e “vai 1” para a próxima posição, quando há um carry-in)

Exemplo:

Vamos somar os números binários 1011 e 1101.

  1011  (equivalente a 11 em decimal)
+ 1101  (equivalente a 13 em decimal)
------

Passo a passo:

1. Coluna da direita (bit menos significativo): 1 + 1 = 10. Escrevemos 0 e “vai 1” para a próxima coluna.
2. Segunda coluna: 1 (do "vai um") + 1 + 0 = 10. Escrevemos 0 e “vai 1” para a próxima coluna.
3. Terceira coluna: 1 (do "vai um") + 0 + 1 = 10. Escrevemos 0 e “vai 1” para a próxima coluna.
4. Quarta coluna: 1 (do "vai um") + 1 + 1 = 11. Escrevemos 1 e “vai 1” para a próxima coluna.
5. Último “vai um”: Como não há mais colunas, o 1 restante é adicionado à esquerda.

  1 1 1  (carries)
  1011
+ 1101
------
 11000  (equivalente a 24 em decimal)

2. Multiplicação Binária: Repetições e Deslocamentos

A multiplicação binária segue um processo análogo à multiplicação decimal. Ela envolve a multiplicação de cada bit do multiplicador pelos bits do multiplicando, seguida pela soma dos produtos parciais, com deslocamentos.

Regras Básicas:

• 0 x 0 = 0
• 0 x 1 = 0
• 1 x 0 = 0
• 1 x 1 = 1

Exemplo:

Vamos multiplicar os números binários 101 e 11.

  101  (equivalente a 5 em decimal)
x  11  (equivalente a 3 em decimal)
----

Passo a passo:

1. Multiplicar 101 por 1 (primeiro dígito do multiplicador, da direita para a esquerda): 101
2. Multiplicar 101 por 1 (segundo dígito do multiplicador), deslocando uma posição para a esquerda: 1010
3. Somar os produtos parciais:

  101
+ 1010
------
 1111  (equivalente a 15 em decimal)

3. Divisão Binária: A Subtração Repetida

A divisão binária é similar à divisão longa que aprendemos no sistema decimal. O processo envolve subtrações repetidas do divisor do dividendo, verificando quantas vezes o divisor “cabe” no dividendo parcial.

Exemplo:

Vamos dividir 1100 por 10.

1100 ÷ 10

Passo a passo:

1. Verifique quantos dígitos do dividendo são necessários para que o divisor “caiba”: 11 (binário) é maior ou igual a 10 (binário).
2. Divida 11 por 10: O quociente é 1.
3. Multiplique o quociente (1) pelo divisor (10): 1 x 10 = 10.
4. Subtraia o resultado do dividendo parcial: 11 - 10 = 01.
5. Baixe o próximo dígito do dividendo (0): O novo dividendo parcial é 010.
6. Divida 010 por 10: O quociente é 1.
7. Multiplique o quociente (1) pelo divisor (10): 1 x 10 = 10.
8. Subtraia o resultado do dividendo parcial: 010 - 10 = 00.
9. Baixe o próximo dígito do dividendo (0): O novo dividendo parcial é 000.
10. Divida 000 por 10: O quociente é 0.

      110  (quociente)
   _______
10 | 1100
   - 10
   ----
    010
   - 10
   ----
     000
    - 00
    ----
      00  (resto)

Portanto, 1100 dividido por 10 é igual a 110 (equivalente a 12 dividido por 2 é igual a 6 em decimal).

4. Conversão de Octal para Binário: Duas Abordagens

Converter um número octal para binário é uma operação comum, especialmente em contextos de programação e sistemas digitais. Existem duas abordagens principais:

Abordagem 1: Via Base 10 (Método mais longo, mas válido)

Este método envolve converter o número octal para sua representação decimal e, em seguida, converter o número decimal para binário.

Exemplo: Converter 27 (octal) para binário.

1. Octal para Decimal:27 (octal) = (2 * 8^1) + (7 * 8^0)= (2 * 8) + (7 * 1)= 16 + 7= 23 (decimal)
2. Decimal para Binário: Dividimos 23 sucessivamente por 2 e anotamos os restos: 23 ÷ 2 = 11 (resto 1) 11 ÷ 2 = 5 (resto 1) 5 ÷ 2 = 2 (resto 1) 2 ÷ 2 = 1 (resto 0) 1 ÷ 2 = 0 (resto 1)Lendo os restos de baixo para cima: 10111 (binário).Portanto, 27 (octal) = 10111 (binário).

Abordagem 2: Conversão Direta (Método mais eficiente)

A forma mais direta e comum de converter octal para binário é converter cada dígito octal diretamente para seu equivalente binário de três bits. Isso é possível porque 8 é uma potência de 2 (2^3 = 8).

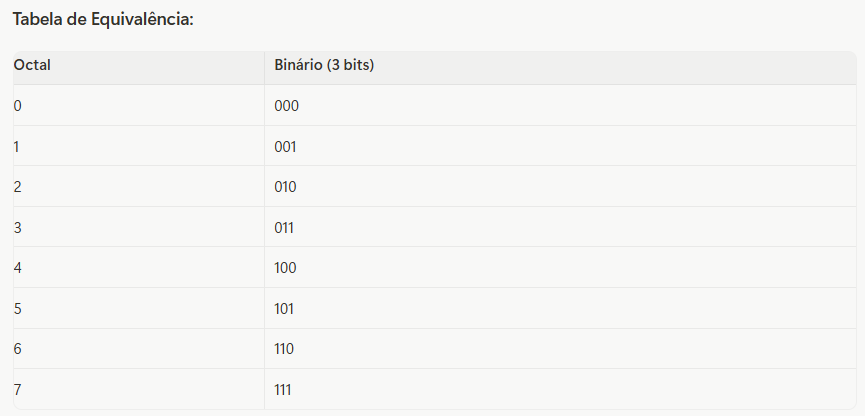
Exemplo: Converter 27 (octal) para binário.

1. Converta cada dígito octal individualmente:
   • 2 (octal) = 010 (binário)
   • 7 (octal) = 111 (binário)
2. Junte os resultados: 010111 (binário).Portanto, 27 (octal) = 010111 (binário). Note que o zero à esquerda pode ser omitido, resultando em 10111.

Glossário

Este glossário define os termos chave relacionados ao sistema binário, suas operações aritméticas e a conversão entre diferentes bases numéricas.

• Base (Numérica): O número de dígitos ou símbolos distintos que um sistema numérico utiliza para representar números. Por exemplo, o sistema decimal tem base 10 (0-9), o binário tem base 2 (0-1) e o octal tem base 8 (0-7).
• Binário: Um sistema numérico de base 2, que utiliza apenas dois dígitos: 0 e 1. É a linguagem fundamental dos computadores e sistemas digitais.
• Bit: Contração de “binary digit” (dígito binário). É a menor unidade de informação em um sistema digital, representando um 0 ou um 1.
• Carry (Vai Um): Em operações de soma (como a soma binária), o “carry” é o dígito que é “levado” para a próxima posição de maior valor quando a soma dos dígitos em uma coluna excede a capacidade da base. No binário, 1 + 1 resulta em 0 com um carry de 1.
• Conversão de Base: O processo de transformar um número de uma base numérica para outra, mantendo o mesmo valor. Por exemplo, converter um número decimal para binário ou um octal para binário.
• Decimal: O sistema numérico de base 10, o mais comum no dia a dia, que utiliza dez dígitos (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).
• Dígito Mais Significativo (MSB – Most Significant Bit): O bit (ou dígito) mais à esquerda em um número binário (ou em qualquer sistema numérico), que possui o maior valor posicional.
• Dígito Menos Significativo (LSB – Least Significant Bit): O bit (ou dígito) mais à direita em um número binário (ou em qualquer sistema numérico), que possui o menor valor posicional.
• Divisão Binária: A operação aritmética de divisão realizada com números no sistema binário, análoga à divisão longa no sistema decimal.
• Multiplicação Binária: A operação aritmética de multiplicação realizada com números no sistema binário, envolvendo a soma de produtos parciais deslocados.
• Octal: Um sistema numérico de base 8, que utiliza oito dígitos (0, 1, 2, 3, 4, 5, 6, 7). É frequentemente usado como uma forma compacta de representar números binários, pois cada dígito octal corresponde a exatamente três bits binários.
• Operações Aritméticas: As operações matemáticas básicas (soma, subtração, multiplicação e divisão) aplicadas a números. No contexto, referem-se a essas operações realizadas no sistema binário.
• Soma Binária: A operação aritmética de adição realizada com números no sistema binário, seguindo regras específicas para 0s e 1s e o conceito de “carry”.

GLOSSÁRIO

Abordagem Direta (Octal → Binário)
Método de conversão em que cada dígito octal é trocado por um grupo de três bits (binário) equivalente. É rápido porque 8 é potência de 2, então não há contas intermediárias em decimal.

Abordagem via Base 10
Forma de conversão em duas etapas: primeiro transforma o número da base de origem (ex.: octal) para decimal; depois, do decimal para binário. Funciona, mas costuma ser mais demorada.

Base (numérica)
Quantidade de símbolos usados para formar números em um sistema. No decimal a base é 10 (0–9); no binário é 2 (0 e 1); no octal é 8 (0–7).

Binário
Sistema numérico de base 2 que usa apenas os dígitos 0 e 1. É o “idioma” dos circuitos digitais, pois representa estados de desligado (0) e ligado (1).

Bit
Contração de “binary digit”. É a menor unidade de informação digital e pode assumir apenas dois valores: 0 ou 1.

Carry (Vai Um)
Dígito “carregado” para a coluna seguinte quando a soma em uma posição excede a capacidade da base. No binário, 1 + 1 gera 0 na coluna e “vai 1” para a próxima.

Carry-in (Entrada de Carry)
Vai-um que já chega a uma coluna por conta de uma soma anterior. Ele deve ser somado aos dígitos daquela posição.

Conversão de Base
Processo de representar o mesmo valor numérico em bases diferentes (ex.: de octal para binário), sem alterar o valor representado.

Decimal
Sistema de base 10, usado no dia a dia. Serve como referência para explicar outros sistemas, mas não é o sistema interno dos computadores.

Deslocamento (Shift)
Movimento dos bits para a esquerda ou direita. Em multiplicações binárias, deslocar à esquerda equivale a “multiplicar por 2” a cada posição.

Dígito Mais Significativo (MSB)
Bit mais à esquerda de um número binário. Tem maior peso posicional dentro do número.

Dígito Menos Significativo (LSB)
Bit mais à direita de um número binário. Tem menor peso posicional e é o primeiro a ser somado ou analisado.

Dividendo
Número que será dividido em uma operação de divisão. Na “divisão longa”, é o número dentro da “chave”.

Divisor
Número pelo qual o dividendo é dividido. Na “divisão longa”, fica à esquerda da “chave”.

Divisão Binária
Operação de divisão usando números binários. O processo é análogo ao decimal: compara, subtrai e “abaixa” o próximo dígito até formar o quociente e o resto.

Multiplicação Binária
Operação que soma produtos parciais formados ao multiplicar cada bit do multiplicador pelos bits do multiplicando, com os devidos deslocamentos.

Multiplicador
Número que multiplica o multiplicando. No método manual, seus bits definem quais linhas de produtos parciais existirão.

Multiplicando
Número que será multiplicado. Seus bits são replicados (ou não) nos produtos parciais conforme os bits do multiplicador.

Números Binários
Valores representados exclusivamente por 0 e 1. Cada posição corresponde a uma potência de 2 (1, 2, 4, 8, 16, …).

Octal
Sistema de base 8 (0–7). É compacto para representar binário, pois cada dígito octal equivale exatamente a três bits.

Operações Aritméticas
Conjunto de operações básicas (soma, subtração, multiplicação e divisão). No binário, seguem regras próprias para 0 e 1 e uso de carry.

Potência de 2
Valores como 1, 2, 4, 8, 16, 32… que definem os pesos das posições em binário. A relação 2³ = 8 explica por que octal “encaixa” em grupos de três bits.

Produtos Parciais
Linhas intermediárias geradas na multiplicação binária ao multiplicar o multiplicando por cada bit do multiplicador, com os deslocamentos adequados.

Quociente
Resultado principal de uma divisão. Em binário, é construído bit a bit conforme os testes de “cabe ou não cabe”.

Resto (ou Resíduo)
Valor que sobra após a divisão. Em binário, indica quanto faltou para o divisor “caber” perfeitamente no último passo.

Sistema Binário
Sistema de base 2 usado em hardware digital. Cada bit reflete um estado lógico (0/1), facilitando implementação física com eletrônica.

Soma Binária
Adição em base 2, feita bit a bit a partir do LSB, aplicando as regras de 0 e 1 e propagando o carry quando necessário.

Subtração (Repetida) na Divisão
Ideia central da divisão longa: subtrair repetidamente um múltiplo do divisor do dividendo parcial para construir o quociente.

Tríade de Bits (Grupo de 3)
Bloco de três bits usado para mapear diretamente um dígito octal (0–7) em binário. Ex.: 7₈ ↔ 111₂.

Valor Posicional
Peso de cada coluna em um número de acordo com a base. Em binário, as posições valem 1, 2, 4, 8… a partir do LSB rumo ao MSB.

FAQ – Perguntas Frequentes

P: Qual é a principal diferença entre a soma binária e a decimal?
R: Na soma binária só existem 0 e 1, então 1 + 1 resulta em 0 na coluna e “vai 1” para a próxima. No decimal, os dígitos vão de 0 a 9 e o vai-um ocorre quando a soma passa de 9.

P: Por que o “vai um” (carry) é tão importante em binário?
R: Porque ele garante que o resultado respeite a base 2. Sempre que a soma em uma coluna excede 1, o excesso é carregado para a próxima coluna, mantendo o valor correto.

P: Como verificar rapidamente se minha multiplicação binária está coerente?
R: Converta os fatores e o produto para decimal (ou use estimativa de potências de 2) e veja se o resultado bate. Outra dica é conferir se os deslocamentos dos produtos parciais estão alinhados.

P: O que significa “deslocar à esquerda” durante a multiplicação binária?
R: Significa adicionar um zero à direita do número em binário, equivalente a multiplicar por 2 a cada deslocamento feito.

P: Na divisão binária, como decido se “cabe” subtrair o divisor do dividendo parcial?
R: Compare os comprimentos (bits) e os valores; se o dividendo parcial for maior ou igual ao divisor, “cabe” e você registra 1 no quociente para aquela etapa.

P: O que é mais eficiente para converter octal em binário: via decimal ou direto?
R: A conversão direta é mais eficiente. Basta trocar cada dígito octal por três bits. A via decimal é útil para conferência ou quando você já está trabalhando em decimal.

P: Por que octal é conveniente para quem estuda eletrônica/aviônicos?
R: Porque cada dígito octal corresponde exatamente a três bits, tornando a leitura e a escrita de números binários mais compactas e menos propensas a erro.

P: MSB e LSB influenciam na ordem de cálculo?
R: Sim. Na soma, você começa pelo LSB (direita) e propaga o carry em direção ao MSB (esquerda). Em operações e comparações, saber quem é MSB/LSB ajuda a entender o peso de cada posição.

P: Como evitar erros comuns na soma binária?
R: Escreva os carries acima das colunas, some sempre da direita para a esquerda e revise cada coluna conferindo se aplicou corretamente as regras 0+0, 0+1, 1+0 e 1+1.

P: Na multiplicação, quando um produto parcial é zero?
R: Quando o bit do multiplicador é 0. Nesse caso, a linha correspondente é 0 e você apenas considera o deslocamento para alinhar com as demais linhas.

P: O que indica um resto diferente de zero após a divisão binária?
R: Indica que o divisor não “cabe” um número inteiro de vezes no dividendo. O resto é o que sobrou após subtrair o maior múltiplo possível do divisor.

P: Qual a melhor estratégia para treinar para a prova ANAC (módulo aviônicos) nesse tema?
R: Pratique somas com carries, multiplicações com produtos parciais e deslocamentos e divisões no esquema longo. Inclua conversões octal↔binário diretas para ganhar velocidade e confiança.