Lei de Avogadro
A Lei de Avogadro estabelece que volumes iguais de gases diferentes, mantidos sob a mesma temperatura e pressão, contêm o mesmo número de moléculas. Proposta pelo físico italiano Amedeo Avogadro, essa teoria foi confirmada por meio de experimentos e fundamentada na teoria cinética dos gases. A lei desempenha um papel essencial na compreensão das propriedades dos gases, sendo uma das bases da química e da termodinâmica. Ela permite calcular volumes molares e entender o comportamento dos gases em condições padrão, sendo fundamental no desenvolvimento de equações de estado e estudos químicos quantitativos.
- Áreas diferenciais
<body> <h1>Áreas diferenciais em sistemas hidráulicos</h1> <p> Um pistão diferencial é projetado para operar com diferentes áreas efetivas em cada lado. No caso apresentado, o pistão em um cilindro hidráulico recebe pressão por ambos os lados, mas a força gerada em cada lado varia devido à diferença nas áreas das faces do pistão. </p> <p> A área de uma das faces corresponde à área total do cilindro. No exemplo, é especificado como sendo 6 polegadas quadradas. A outra face, no entanto, possui uma área reduzida devido à presença da haste do pistão, que ocupa parte do espaço, resultando em uma área efetiva menor, de 4 polegadas quadradas (6 menos os 2 ocupados pela haste). </p> <p> A pressão aplicada nas duas faces é igual, no exemplo, 20 psi. Dessa forma, a força em cada direção pode ser calculada pela multiplicação da pressão pela área da respectiva face: </p> <ul> <li>Força para a direita: 20 psi × 6 in² = 120 lbf</li> <li>Força para a esquerda: 20 psi × 4 in² = 80 lbf</li> </ul> <p> A diferença de forças gera um desequilíbrio de 40 libras-força, empurrando o pistão para a direita. Esse princípio reflete como o projeto de áreas diferenciais pode ser usado para controlar movimento e força nos sistemas hidráulicos, aproveitando a vantagem mecânica inerente. </p> </body> </html> - Multiplicação de forças
<body <h1Multiplicação de Forças</h1 <pO conceito apresentado baseia-se na <strongLei de Pascal</strong, segundo a qual a pressão exercida em um fluido incompressível é transmitida uniformemente para todas as partes do fluido. Esse princípio permite o funcionamento de sistemas hidráulicos que multiplicam forças, como ilustrado nos exemplos descritos:</p <h21. Área dos pistões</h2 <pQuando dois pistões têm áreas diferentes, a força aplicada a um dos pistões resulta em uma pressão transmitida igualmente pelo fluido ao outro pistão. A pressão é calculada pela fórmula:</p <p<strongPressão (p.s.i.) = Força aplicada (libras) / Área do pistão (polegadas quadradas)</strong</p <h22. Exemplo de multiplicação de forças</h2 <ul <li<strongPistão de entrada:</strong área = 2 in², força aplicada = 20 libras.</li <li<strongPressão gerada no fluido:</strong 10 p.s.i. (20 / 2).</li <li<strongPistão de saída:</strong área = 20 in².</li <li<strongForça gerada no pistão de saída:</strong 200 libras (10 x 20).</li </ul <h23. Inversão do sistema</h2 <pSe os papéis dos pistões forem invertidos (o maior como entrada e o menor como saída), a força de saída será proporcionalmente reduzida. Por exemplo, com uma razão de áreas de 10:1, a força de saída será 1/10 da força de entrada.</p <h24. Razão constante</h2 <pA razão entre a força de saída e a força de entrada é constante, dependendo apenas da relação entre as áreas dos pistões.</p <h25. Aplicações práticas</h2 <ul <li<strongGanho mecânico:</strong Utilizado em dispositivos como freios hidráulicos e elevadores, onde pequenas forças aplicadas em áreas pequenas geram forças muito maiores em áreas maiores.</li <li<strongPerda de movimento:</strong A amplitude do movimento do pistão maior será inversamente proporcional ao ganho de força.</li </ul <pEste princípio é fundamental para sistemas que requerem multiplicação de... - Pressão e força em um fluido num sistemade potência
<body <h1Pressão e Força em um Fluido</h1 <p De acordo com a <strongLei de Pascal</strong, a pressão exercida em um ponto de um fluido em equilíbrio é transmitida igualmente em todas as direções e por todo o fluido, independentemente do formato do recipiente. Este princípio é fundamental em sistemas de potência hidráulica e mecânica. </p <h2Aplicação em Sistemas Hidráulicos</h2 <p Quando uma força é aplicada a um fluido confinado, como em um sistema com pistões, essa pressão é distribuída uniformemente. Por exemplo: </p <ol <li <strongPressão Gerada:</strong <p Se um pistão com área de 10 polegadas quadradas recebe uma força de 100 libras, a pressão no fluido será: </p <p <emPressão (p.s.i.)</em = <emForça (libras)</em / <emÁrea (pol²)</em = 100 / 10 = 10 p.s.i. </p </li <li <strongTransmissão de Força:</strong <p A pressão gerada no fluido age sobre outro pistão com a mesma área (10 pol²), aplicando uma força de 10 libras por polegada quadrada em toda sua superfície, resultando na transmissão de 100 libras de força. </p </li </ol <h2Modificações no Sistema</h2 <p A forma do recipiente ou as conexões entre os pistões não afetam a transmissão de força, desde que o fluido esteja confinado e a passagem esteja desobstruída. Um exemplo é a substituição do tubo reto por um de seção reduzida ou curvado, sem alterações na eficácia da transmissão de pressão. </p <h2Exemplos Práticos</h2 <p Sistemas hidráulicos em aeronaves, como os freios ou acionamento de flaps, utilizam o princípio da Lei de Pascal para converter forças pequenas em grandes forças operacionais, com precisão e eficiência. Além disso, esses sistemas permitem o uso de tubos estreitos ou formas específicas de recipientes para atender às... - Calculando força, pressão e área
<body> <h1>Força, Pressão e Área</h1> <p> O cálculo da relação entre força, pressão e área é fundamental em sistemas de força fluida, como os hidráulicos, e segue os princípios da Lei de Pascal. As fórmulas derivadas dessa relação são: </p> <h2>1. Força</h2> <p> Representada por <strong>F</strong>, é o produto da pressão <strong>P</strong> pela área <strong>A</strong>: </p> <pre>F = P × A</pre> <h2>2. Pressão</h2> <p> Representada por <strong>P</strong>, é a força dividida pela área: </p> <pre>P = F / A</pre> <h2>3. Área</h2> <p> Representada por <strong>A</strong>, é a força dividida pela pressão: </p> <pre>A = F / P</pre> <p> Estas fórmulas são interdependentes e frequentemente ilustradas em diagramas de triângulos, permitindo que qualquer uma das variáveis seja resolvida em função das outras duas. </p> <h2>Área em Superfícies Circulares</h2> <p> Quando a área a ser calculada é circular, a fórmula aplicada é: </p> <pre>A = πr²</pre> <p> Aqui, <strong>r</strong> é o raio do círculo, e <strong>π</strong> é aproximadamente 3,1416. O raio deve ser medido nas mesmas unidades em que se deseja expressar a área. </p> <h2>Aplicação</h2> <p> Nos sistemas hidráulicos, essas fórmulas são essenciais para projetar dispositivos como pistões ou atuadores, otimizando força e eficiência. Por exemplo, ao aumentar a área de um pistão, a força gerada para a mesma pressão aplicada também aumenta proporcionalmente, conforme demonstrado no conceito de ganho mecânico. </p> </body> </html> - Força e Pressão
Força e Pressão
A força é uma interação que pode ser descrita como um empurrar ou puxar aplicado a uma superfície, sendo medida em unidades como libras (lb) ou Newtons (N). A pressão, por outro lado, é a quantidade de força distribuída por uma área específica, representada em libras por polegada quadrada (psi) ou Pascais (Pa).
De acordo com a Lei de Pascal, em sistemas hidráulicos e pneumáticos, uma pressão aplicada em um ponto de um fluido em equilíbrio é transmitida de forma igual para todas as partes do fluido e às superfícies de contato do sistema. Isso permite multiplicar forças: uma pequena força aplicada em uma área menor pode gerar uma força muito maior em uma área maior.
Por exemplo, um sistema hidráulico utiliza esse princípio para realizar trabalho pesado, como levantar cargas em aeronaves ou acionar flaps e trens de pouso. A precisão desses sistemas se deve ao fato de os fluidos hidráulicos serem praticamente incompressíveis.
- Lei de Pascal
Lei de Pascal
A Lei de Pascal estabelece que a pressão aplicada a um ponto de um fluido em equilíbrio é transmitida igualmente em todas as direções dentro do fluido e atua perpendicularmente às superfícies do recipiente. Esse princípio é fundamental para os sistemas hidráulicos e pneumáticos utilizados em aviação e outras indústrias.
Quando uma força é aplicada a um fluido incompressível em um recipiente fechado, a pressão gerada distribui-se uniformemente. Por exemplo, se um peso de 8 libras em uma área de 1 polegada quadrada no fundo de um tanque exerce uma pressão de 8 psi, essa pressão será a mesma em todos os pontos do mesmo nível dentro do fluido. Isso ocorre porque o líquido, em repouso, mantém um equilíbrio de pressões em todas as direções.
A pressão em um sistema depende da densidade do fluido e da altura da coluna de líquido acima do ponto de medição. Por exemplo, para gerar 8 psi, seriam necessários 222 polegadas de altura de água ou 252 polegadas de óleo, pois a densidade dos fluidos varia.
A aplicação prática da Lei de Pascal pode ser vista nos sistemas hidráulicos, onde uma força pequena aplicada em um ponto pode ser amplificada para realizar trabalhos maiores. Exemplos incluem freios hidráulicos e mecanismos de retração de trem de pouso em aeronaves.
- Transmissão de Forças por Fluidos
Transmissão de Forças por Fluidos
O transporte de força através de fluidos, baseado na Lei de Pascal, estabelece que uma pressão aplicada em um ponto de um fluido em equilíbrio se transmite igualmente em todas as direções, sem redução. Este princípio é fundamental em sistemas hidráulicos, como os usados em aeronaves e outros equipamentos.
Transmissão em Materiais Sólidos
Quando uma força é aplicada em uma extremidade de uma barra rígida, ela é transferida quase integralmente para a outra extremidade, seguindo a direção inicial da aplicação. Quanto mais rígida a barra, menor a dissipação da força em ângulos retos, e mais eficiente é a transmissão para o ponto oposto.
Transmissão em Fluidos
Ao aplicar uma força a um líquido confinado, a pressão resultante se distribui uniformemente para todos os lados dentro do recipiente. Isso significa que:
- A força se transmite não apenas na direção aplicada, mas também para todas as superfícies de contato.
- O recipiente se enche de pressão uniforme, refletindo o comportamento incompressível dos líquidos.
No caso de gases, que são compressíveis, a força é transmitida de maneira semelhante, mas com uma rigidez muito menor. Isso ocorre porque os gases permitem uma maior compressão e variação de volume, ao contrário dos líquidos que mantêm sua densidade constante.
Aplicações Práticas
Este conceito é a base para sistemas hidráulicos e pneumáticos:
- Em sistemas hidráulicos, utiliza-se a incompressibilidade dos líquidos para operar controles pesados, como os de trem de pouso ou flaps em aeronaves.
- Nos sistemas pneumáticos, o ar comprimido substitui o líquido, sendo ideal para aplicações que requerem menor força ou maior flexibilidade operacional.
Esses princípios destacam as diferenças fundamentais na utilização de líquidos e gases, com líquidos sendo preferidos em sistemas que requerem força estável e precisa.
- Transmissão de forças através de fluídos
Transmissão de Forças por Fluidos
O transporte de força através de fluidos, baseado na Lei de Pascal, estabelece que uma pressão aplicada em um ponto de um fluido em equilíbrio se transmite igualmente em todas as direções, sem redução. Este princípio é fundamental em sistemas hidráulicos, como os usados em aeronaves e outros equipamentos.
Transmissão em Materiais Sólidos
Quando uma força é aplicada em uma extremidade de uma barra rígida, ela é transferida quase integralmente para a outra extremidade, seguindo a direção inicial da aplicação. Quanto mais rígida a barra, menor a dissipação da força em ângulos retos, e mais eficiente é a transmissão para o ponto oposto.
Transmissão em Fluidos
Ao aplicar uma força a um líquido confinado, a pressão resultante se distribui uniformemente para todos os lados dentro do recipiente. Isso significa que:
- A força se transmite não apenas na direção aplicada, mas também para todas as superfícies de contato.
- O recipiente se enche de pressão uniforme, refletindo o comportamento incompressível dos líquidos.
No caso de gases, que são compressíveis, a força é transmitida de maneira semelhante, mas com uma rigidez muito menor. Isso ocorre porque os gases permitem uma maior compressão e variação de volume, ao contrário dos líquidos que mantêm sua densidade constante.
Aplicações Práticas
Este conceito é a base para sistemas hidráulicos e pneumáticos:
- Em sistemas hidráulicos, utiliza-se a incompressibilidade dos líquidos para operar controles pesados, como os de trem de pouso ou flaps em aeronaves.
- Nos sistemas pneumáticos, o ar comprimido substitui o líquido, sendo ideal para aplicações que requerem menor força ou maior flexibilidade operacional.
Esses princípios destacam as diferenças fundamentais na utilização de líquidos e gases, com líquidos sendo preferidos em sistemas que requerem força estável e precisa.
- Lei de Dalton
Lei de Dalton
A Lei de Dalton, proposta pelo físico inglês John Dalton, descreve o comportamento da pressão em misturas de gases que não reagem quimicamente. Quando diferentes gases são colocados juntos em um recipiente, cada gás se espalha por todo o volume disponível, exercendo uma pressão parcial. A pressão parcial é a pressão que cada gás individual exerceria se ocupasse sozinho o espaço total.
Essa relação é regida pela fórmula:
Pressão total = Soma das pressões parciais de todos os gases presentes.
A redução da pressão de cada gás no espaço da mistura segue a Lei de Boyle, que trata da relação entre pressão e volume para gases a temperatura constante. A Lei de Dalton é fundamental em diversos campos, incluindo a aviação, onde o comportamento dos gases sob diferentes pressões é relevante, como no sistema de pressurização da cabine ou na análise de gases de combustão.
Em resumo, a Lei de Dalton afirma que a pressão total de uma mistura de gases é a soma das pressões parciais de cada gás, assumindo que eles não interagem quimicamente e que todos estão à mesma temperatura e ocupam o mesmo volume.
- Lei geral dos gases
<body <h1Lei Geral dos Gases</h1 <p A Lei Geral dos Gases é uma fórmula que unifica as Leis de Boyle e Charles, permitindo relacionar as variáveis pressão (<emP</em), volume (<emV</em) e temperatura (<emT</em) de um gás ideal. É expressa matematicamente como: </p <p <strongFórmula:</strong<br <code(P1 * V1) / T1 = (P2 * V2) / T2</code </p <p Nessa fórmula: <ul <li<codeP1</code e <codeP2</code: representam as pressões absolutas nos estados inicial e final.</li <li<codeV1</code e <codeV2</code: são os volumes do gás nos estados inicial e final.</li <li<codeT1</code e <codeT2</code: são as temperaturas absolutas (em Kelvin ou Rankine) nos estados inicial e final.</li </ul </p <h2Aplicações</h2 <ol <li<strongTransformação Isotérmica:</strong Quando a temperatura (<codeT1 = T2</code) é constante, a fórmula reduz-se à Lei de Boyle: <codeP1 * V1 = P2 * V2</code.</li <li<strongTransformação Isocórica:</strong Quando o volume (<codeV1 = V2</code) é constante, a fórmula simplifica-se para a relação direta entre pressão e temperatura: <codeP1 / T1 = P2 / T2</code.</li <li<strongTransformação Isobárica:</strong Com pressão constante (<codeP1 = P2</code), a relação entre volume e temperatura segue a Lei de Charles: <codeV1 / T1 = V2 / T2</code.</li </ol <h2Gases Ideais</h2 <p Essa lei aplica-se com maior precisão aos gases ideais, em que as moléculas são elásticas e ocupam um volume desprezível. Na prática, é suficientemente precisa para descrever o comportamento de gases reais em condições não extremas de pressão e temperatura. </p <h2Exemplos de Cálculo</h2 <h3Exemplo 1: Determinar a pressão final</h3 <p <strongCondições iniciais:</strong<br <codeV1 = 2 ft³, P1 = 75 psi, T1 = 540 R</code<br <strongCondições finais:</strong<br ... - Exemplos da lei de Charles:
<body> <h1>Lei de Charles</h1> <p>A Lei de Charles descreve a relação direta entre temperatura e pressão ou volume de um gás quando o outro parâmetro é mantido constante. No exemplo do cilindro de gás, ao aumentar a temperatura de 70ºF para 130ºF, observa-se o impacto direto no aumento da pressão interna do cilindro, confirmando essa relação.</p> <h2>Cálculo</h2> <p>Para calcular a nova pressão (P2) em um sistema usando a Lei de Charles, é necessário converter temperatura e pressão para escalas absolutas. Em temperaturas absolutas (Rankine), 70°F se torna 530°R e 130°F equivale a 590°R. A fórmula utilizada é:</p> <pre> P1 / T1 = P2 / T2 </pre> <p>Substituindo valores:</p> <pre> (1800 + 14,7) / 530 = P2 / 590 </pre> <p>Resolvendo, P2 é obtido como 2020 psi (absoluto). Subtraindo a pressão atmosférica padrão (14,7 psi), resulta em uma pressão indicada de 2005,3 psi.</p> <h2>Aplicações Práticas</h2> <p>Aplicações práticas da Lei de Charles são frequentes na aviação, como na análise de gases em tanques de combustível, comportamento atmosférico na estratosfera, e no impacto de variações de temperatura em instrumentos sensíveis, aumentando a segurança operacional.</p> </body> </html> - Lei de Charles
<body> <h1>Lei de Charles</h1> <p>Jacques Charles, cientista francês, fez contribuições significativas à teoria cinética dos gases. Ele descobriu que o volume de um gás varia diretamente com sua temperatura absoluta, desde que a pressão seja mantida constante. Este princípio é conhecido como <strong>Lei de Charles</strong>.</p> <p>Na forma de equação, a relação é expressa como:</p> <p><code>V<sub>1</sub> / T<sub>1</sub> = V<sub>2</sub> / T<sub>2</sub></code></p> <p>ou</p> <p><code>V<sub>1</sub> · T<sub>2</sub> = V<sub>2</sub> · T<sub>1</sub></code></p> <ul> <li><strong>V</strong> representa o volume do gás.</li> <li><strong>T</strong> é a temperatura absoluta, medida em Kelvin (K).</li> <li>Os índices 1 e 2 referem-se a estados diferentes do gás.</li> </ul> <p>Essa fórmula demonstra que, se o volume de um gás aumenta, sua temperatura absoluta também deve aumentar proporcionalmente, e o inverso ocorre se o volume diminuir, assumindo que a pressão permanece constante.</p> <h2>Aplicação</h2> <p>Este conceito é amplamente utilizado em termodinâmica para prever comportamentos de gases em condições variáveis, sendo fundamental em áreas como engenharia aeronáutica e sistemas de pressurização.</p> <h2>Observação</h2> <p>Em casos de volume constante, a Lei de Charles também implica que a pressão de um gás varia diretamente com sua temperatura absoluta. Este comportamento é descrito em outras formulações da teoria dos gases.</p> </body> </html> - Lei de Boyle
<body <h1Lei de Boyle</h1 <pA compressibilidade é uma característica fundamental dos gases. O cientista inglês Robert Boyle realizou experimentos que resultaram na formulação da Lei de Boyle, que descreve a relação entre pressão e volume de um gás mantido a temperatura constante. Ele observou que, ao dobrar a pressão exercida sobre uma amostra fixa de gás, o volume reduzia-se à metade, e quando a pressão diminuía, o volume aumentava proporcionalmente.</p <h2Definição e Fórmula</h2 <pA Lei de Boyle estabelece que, para um gás ideal em temperatura constante, o produto da pressão (P) e do volume (V) permanece constante:</p <p<strongP<sub1</sub · V<sub1</sub = P<sub2</sub · V<sub2</sub</strong</p <pAqui:</p <ul <li<strongP<sub1</sub</strong e <strongV<sub1</sub</strong são a pressão e o volume iniciais,</li <li<strongP<sub2</sub</strong e <strongV<sub2</sub</strong são a pressão e o volume finais.</li </ul <h2Demonstração Prática</h2 <pA lei pode ser demonstrada aprisionando gás em um cilindro com um pistão móvel. Aplicando força ao pistão para reduzir o volume, a pressão aumenta proporcionalmente. Por exemplo, se o volume de gás é reduzido à metade, a pressão será dobrada.</p <h2Exemplo</h2 <pUm gás de 4 pés cúbicos, sob pressão de 100 psi, expande para um volume de 6 pés cúbicos. Usando a fórmula, a nova pressão (<strongP<sub2</sub</strong) é calculada como:</p <p<strongP<sub2</sub = (P<sub1</sub · V<sub1</sub) / V<sub2</sub</strong</p <pSubstituindo os valores:</p <p<strongP<sub2</sub = (100 · 4) / 6 = 66,6 psi</strong</p <h2Gases Ideais e Aplicações na Aviação</h2 <pUm gás que segue perfeitamente a Lei de Boyle é chamado de gás ideal. Na prática, a densidade de um gás aumenta com a pressão, desde que a temperatura permaneça constante. A Lei de Boyle tem diversas aplicações na aviação, como:</p <ul <liGarrafas de CO<sub2</sub para inflar coletes... - Teoria Cinética dos Gases
Teoria Cinética dos Gases
A teoria cinética dos gases descreve o comportamento dos gases considerando que são compostos por moléculas idênticas em movimento constante e aleatório, agindo como pequenas esferas elásticas separadas por distâncias relativamente grandes. A temperatura do gás determina o grau de movimento dessas moléculas, com o aumento da temperatura causando maior agitação molecular e, consequentemente, mais colisões entre moléculas e com as paredes do recipiente.
Essas colisões explicam propriedades como a pressão, que aumenta em recipientes fechados devido à maior frequência de choques nas paredes, um efeito exemplificado pela elevação da pressão dos pneus em dias quentes. Se o recipiente for elástico, como um balão, ele se expande sob pressão crescente. Em recipientes abertos, o gás se dispersa para o ambiente.
A teoria também considera que a velocidade média das moléculas correlaciona-se à temperatura do gás. Apesar das diferenças de velocidade e direção entre moléculas individuais, a combinação desses movimentos resulta numa velocidade média, que pode ser usada para prever propriedades macroscópicas do gás. Assim, a teoria cinética conecta aspectos microscópicos (movimento molecular) às características macroscópicas observadas nos gases.
- Compressibilidade e Expansão de Gases
Compressibilidade e Expansão de Gases
Os gases possuem características que os diferenciam dos líquidos, principalmente no que diz respeito à compressibilidade e à expansão.
Os líquidos são praticamente incompressíveis, o que significa que suas moléculas estão muito próximas, tornando difícil alterar seu volume mesmo sob pressão significativa. Por outro lado, os gases são altamente compressíveis porque suas moléculas estão espaçadas, permitindo a redução do volume quando submetidos a compressão.
Além disso, os gases têm a propriedade de expandir para ocupar completamente o volume de qualquer recipiente fechado em que sejam colocados. Isso ocorre devido à movimentação livre e rápida de suas moléculas, que se distribuem uniformemente para preencher todo o espaço disponível. Em contraste, os líquidos ocupam apenas o volume correspondente à sua quantidade, sem preencher completamente o recipiente.
Essas propriedades são cruciais para diversas aplicações na engenharia e na aviação. Por exemplo, a compressibilidade dos gases é explorada em sistemas pneumáticos e na compressão em turbinas a gás. A capacidade de expansão dos gases é essencial em sistemas de propulsão e ventilação.
- Operações e Segurança
Operações e Segurança
O uso correto de instrumentos de teste especializados é essencial para a análise de circuitos eletrônicos, mas sua má utilização pode causar danos graves ao equipamento e ao circuito em teste. Operadores devem assegurar que compreendem o funcionamento do instrumento, sua forma de conexão, e verificar se a tensão ou corrente medida está dentro da capacidade do dispositivo.
Impactos no circuito: instrumentos como voltímetros e osciloscópios podem interferir nas condições de operação do circuito. Isso pode levar a leituras incorretas, especialmente em circuitos sensíveis. Assim, o conhecimento detalhado do equipamento e a leitura das instruções do fabricante são fundamentais.
Segurança em circuitos ativos: muitos testes são feitos em circuitos energizados, criando riscos de choques elétricos ou eletrocussão. Seguir práticas seguras minimiza esses perigos:
- Limite a exposição a altas tensões: valores acima de 100 V são considerados perigosos.
- Cuidado com conexões de alta tensão: evite contato com áreas expostas.
- Ambientes isolados: realize testes em locais com isolamento adequado, como pisos isolantes.
- Trabalho com uma mão: mantenha uma mão longe de circuitos e massas elétricas para evitar fechamentos acidentais de circuito através do corpo.
- Desconexão da energia: mesmo desligados, equipamentos podem conter cargas internas; desconecte-os da alimentação para maior segurança.
- Trabalho em equipe: sempre que possível, tenha alguém por perto para ajudar em emergências.
Essas precauções são essenciais para evitar acidentes e garantir a segurança ao trabalhar com circuitos ativos.
- Seção Horizontal
Seção Horizontal
A seção horizontal do osciloscópio controla a taxa de varredura horizontal do display, determinando o intervalo de tempo representado na tela. Isso é essencial para visualizar sinais de entrada em diferentes escalas temporais.
Essa seção inclui o gerador de varredura, que produz uma forma de onda de dente de serra (ou rampa). Essa onda controla o deslocamento do sinal no eixo horizontal, sincronizando o movimento do feixe de varredura (em displays CRT) ou a atualização da imagem (em displays LCD). O gerador é calibrado como base de tempo, permitindo medir o período e, consequentemente, a frequência do sinal.
O operador pode ajustar manualmente a taxa de varredura para adaptar o display ao sinal, ou utilizar um recurso automático para configurar a escala temporal ideal para a análise. Esses controles tornam possível observar detalhes específicos ou padrões gerais do sinal sendo analisado.
- Seção de Gatilho
Seção de Gatilho
A seção de gatilho do osciloscópio controla o início do desenho da forma de onda no display, garantindo que o sinal seja exibido de maneira clara e estável.
Esta seção identifica um ponto específico na forma de onda de entrada, geralmente um nível de tensão predefinido. Quando este ponto é detectado, a seção de gatilho ativa o gerador de varredura horizontal para que o osciloscópio redesenhe a forma de onda a partir do mesmo ponto em cada ciclo.
Sem o gatilho, o display apresentaria formas de onda confusas e instáveis, dificultando a análise do sinal. A sincronização precisa assegurada pela seção de gatilho permite que o operador visualize a forma de onda de maneira consistente e compreensível.
- Seção Vertical
Seção Vertical
A seção vertical do osciloscópio controla o deslocamento do sinal no eixo Y, representando os níveis de tensão da forma de onda medida. Esse eixo reflete a amplitude da tensão em tempo real, enquanto o eixo horizontal (X) representa a variação temporal do sinal.
Nos osciloscópios de CRT, os sinais de entrada são transformados em tensões de deflexão para movimentar o feixe de elétrons verticalmente. Já nos osciloscópios de LCD, as informações verticais são processadas eletronicamente e enviadas ao display por circuitos especializados.
Essa seção também interage diretamente com a seção de gatilho. O engatilhamento sincroniza o gerador de dente de serra (usado na varredura horizontal) com a forma de onda do sinal, garantindo um display estável. Sem a sincronização, a forma de onda ficaria dessincronizada, resultando em sobreposições ou em um sinal que aparenta "se mover" na tela. Para evitar isso, um pulso de gatilho é aplicado ao gerador de dente de serra, podendo vir da seção vertical ou de uma fonte externa.
- Ponta de Prova de Osciloscópio
Ponta de Prova Osciloscópio
As pontas de prova de osciloscópio são componentes essenciais que conectam o circuito testado ao osciloscópio, minimizando interferências e ajustando características elétricas para medições precisas.
Função e Importância: A ponta de prova é responsável por:
- Conectar o circuito ao osciloscópio sem distorcer os sinais.
- Reduzir interferências externas, que podem afetar medições, especialmente em sinais de baixo nível.
- Adaptar características elétricas como impedância, capacitância e indutância, garantindo precisão em frequências altas.
Problemas com Fios Comuns:
- Captam ruídos externos.
- Elevada indutância, inadequada para medições de alta frequência.
Uso de Cabo Coaxial:
- O cabo coaxial é um fio blindado especializado que reduz a indutância e as interferências.
- A ponta de prova compensa a capacitância e a resistência adicionais introduzidas pelo cabo.
Tipos e Configurações Comuns:
- Ponta de Prova 1X e 10X:
- 1X: Mede sinais diretamente.
- 10X: Atenua o sinal em um fator de 10, usando um circuito RC de alta resistência e baixa capacitância, reduzindo o impacto no circuito medido.
- Pontas de Alta Tensão:
- Projetadas para sinais de alta amplitude.
- São fisicamente maiores e possuem isolamento reforçado.
- Pontas Indutivas:
- Não precisam de contato físico direto com o circuito.
- Medem tensões ou correntes alternadas por indução eletromagnética, captando o sinal ao passar o fio pelo captador.
Características Técnicas:
- Carga típica: Capacitância de cerca de 110 pF e resistência de 1 MΩ.
- Cabo coaxial: Criticamente ajustado em projeto e comprimento para uma impedância específica, essencial para medições precisas.
As pontas de prova são projetadas para minimizar a carga sobre o circuito, preservar a integridade do sinal medido e garantir alta confiabilidade em diversas aplicações.
- Categorias de Osciloscópio
Categorias de Osciloscópio
Os osciloscópios são classificados principalmente em analógicos e digitais, com diferenças em tecnologia, processamento e exibição de sinais elétricos.
1. Osciloscópios Analógicos:
- Processamento: Utilizam circuitos analógicos para representar diretamente o sinal de entrada.
- Display: Geralmente possuem um tubo de raios catódicos (CRT) que projeta formas de onda na tela.
- Características:
- Requer ajustes manuais para sinais complexos.
- Adequados para sinais de baixa frequência.
- Desvantagem: Tornaram-se menos comuns devido à limitação de recursos em comparação com os digitais.
2. Osciloscópios Digitais:
- Processamento: Usam microprocessadores para analisar sinais e gerar representações gráficas no display.
- Display: Contêm telas planas de cristal líquido (LCD), sendo mais leves, confiáveis e portáteis.
- Características:
- Processam sinais de frequências mais altas.
- Armazenam dados na memória para análise posterior ou transferência para PC.
- Muitos modelos permitem exportar informações via USB ou conexão sem fio.
- Avanços recentes:
- Integração com PCs, tablets e smartphones, utilizando placas de aquisição de sinal e conexões USB.
3. Diferenças no Display:
- CRT:
- O feixe de elétrons projeta sinais em uma tela fosforescente, criando o movimento vertical e horizontal com placas de deflexão.
- Mais robusto para formas de onda dinâmicas, mas menos comum atualmente.
- LCD:
- Gera imagens digitais usando dados de controle enviados pelo processador do osciloscópio.
- Preferido por sua confiabilidade, custo mais baixo e eficiência energética.
4. Gratícula:
- Uma grade de referência presente na tela para medições de tensão e frequência.
- Pode ser pintada diretamente no CRT ou projetada no LCD como parte da imagem gerada.
Os avanços na tecnologia digital tornaram os osciloscópios modernos mais versáteis, portáteis e fáceis de usar, com maior capacidade de análise...
- OSCILOSCÓPIO
Osciloscópio
O osciloscópio é um instrumento de medição avançado que permite visualizar graficamente sinais elétricos variáveis, medindo a tensão (amplitude) e a frequência (tempo) de um circuito em uma tela bidimensional.
1. Função Principal:
- Medição gráfica: Mostra variações de tensão no eixo vertical (eixo Y) e de tempo no eixo horizontal (eixo X).
- Análise de sinais: Permite identificar sinais constantes ou variáveis, essenciais para circuitos de alta frequência e mutáveis, como sistemas digitais ou de rádio.
2. Aplicações:
- Circuitos rápidos: Útil para sinais que mudam rapidamente, onde multímetros comuns são insuficientes.
- Comparação de sinais: Osciloscópios multitraço permitem analisar e comparar dois ou mais sinais simultaneamente.
- Medição de fenômenos não elétricos: Com transdutores, o osciloscópio pode medir sons, temperaturas e outras formas de energia convertidas em sinais elétricos.
3. Funcionamento Básico:
- Conexão: Feita por pontas de prova ou sondas especializadas que captam os sinais do circuito.
- Representação gráfica: Processa o sinal medido e gera uma imagem no display (tubo CRT ou tela LCD).
- Componentes principais:
- Bloco de entrada: Amplifica ou atenua o sinal recebido.
- Seção vertical: Ajusta a escala de tensão no eixo Y.
- Seção horizontal: Configura o intervalo de tempo no eixo X.
- Gatilho: Sincroniza o sinal para uma visualização estável.
- Processador de saída: Converte os dados em uma imagem interpretável.
4. Formas de Onda:
- A tela pode exibir diferentes formas de onda, como senoidais, quadradas ou triangulares, representando a natureza dos sinais no circuito.
5. Importância em Manutenção de Aeronaves:
- Diagnóstico de sistemas aviônicos avançados e circuitos eletrônicos complexos.
- Teste e análise de sinais de rádio e comunicação.
- Verificação de sistemas digitais de alta velocidade.
O osciloscópio é uma ferramenta indispensável para técnicos...
- Contadores de Frequência
Contadores de Frequência
Os contadores de frequência são instrumentos utilizados para medir a frequência de sinais elétricos em circuitos de corrente alternada (CA) ou pulsante, convertendo os pulsos elétricos em valores numéricos precisos.
1. Funcionamento:
- Princípio de operação:
- Transformam a forma de onda de entrada em uma onda quadrada padrão com a mesma frequência.
- Comparam a frequência da onda padrão com uma frequência de referência interna, determinando o valor medido.
- Medição média:
- Utilizam circuitos de porta de tempo para medir a frequência média do sinal em períodos pré-determinados.
- Um tempo de porta típico é de 1 segundo.
2. Aplicações:
- Medem a frequência de:
- Corrente alternada (CA).
- Corrente contínua pulsante.
- Formas de onda quadradas ou triangulares.
- Usados em testes de sistemas de transmissão, sinais digitais e circuitos de alta precisão.
3. Conexão ao Circuito:
- Conectados em paralelo ao circuito, permitindo monitorar a tensão sem interferir diretamente na operação.
4. Importância em Manutenção de Aeronaves:
- Diagnóstico de sistemas de comunicação e navegação, que dependem de frequências precisas.
- Verificação de circuitos eletrônicos pulsantes em aviônicos modernos.
Os contadores de frequência são indispensáveis para medições precisas em circuitos eletrônicos e elétricos, especialmente em sistemas que demandam estabilidade e controle de sinais frequenciais.
- Princípio de operação:
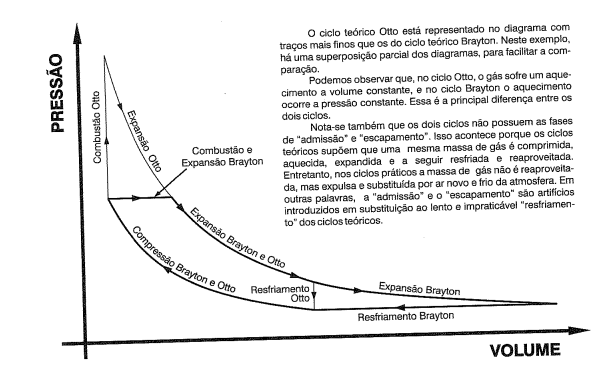
- Ciclo Brayton e Ciclo Otto
Ciclo Otto: Adotado em motores a pistão, o ciclo Otto é caracterizado por uma combustão instantânea que ocorre sob volume constante. A expansão do gás resultante move o pistão até o ponto morto inferior (PMB). Após a expansão, o gás é resfriado rapidamente à temperatura ambiente, completando o ciclo.
Ciclo Brayton: Utilizado em turborreatores e estatorreatores, neste ciclo a combustão ocorre gradualmente e à pressão constante, enquanto o gás se expande. Após a combustão, o gás continua a se expandir, mas a pressão diminui gradualmente até se equilibrar com a pressão ambiente. O resfriamento do gás ocorre também a pressão constante antes do ciclo se completar.
As principais diferenças entre os dois ciclos estão na forma como a combustão e a expansão do gás acontecem, com o Brayton priorizando gradatividade e pressão constante, enquanto o Otto apresenta mudanças bruscas em volume constante.
Essas diferenças refletem diretamente no funcionamento dos motores a que os ciclos se aplicam, sendo o Ciclo Brayton essencial para a eficiência de motores a reação, devido à natureza contínua da entrada e saída de gases em alta velocidade e eficiência térmica.
Livro Aeronaves e Motores – Conhecimentos Técnicos de Avião – Jorge M. Homa - Cálculo da Tração
Cálculo da Tração - Motores Turbojato Cálculo da Tração em Motores Turbojato
Em motores turbojato, a tração pode ser calculada de modo aproximado utilizando a fórmula abaixo:
T = P × (A) + (W × (V2 - V1)) ÷ gSignificado dos Símbolos
- T: Tração (força gerada pelo motor, geralmente em libras-força ou quilogramas-força).
- P: Pressão na saída do bocal propulsor.
- PO: Pressão atmosférica (externa ao motor).
- A: Área na saída do bocal propulsor.
- W: Fluxo em peso do ar que passa pelo motor.
- V2: Velocidade dos gases na saída do bocal de escape.
- V1: Velocidade do ar de admissão na entrada do motor.
- g: Aceleração da gravidade (9,81 m/s²).
Considerações Adicionais
Para outros tipos de motores, que não são turbojatos, o cálculo da tração pode ser mais complexo ou exigir gráficos experimentais. Nestes casos, as características do motor e suas condições operacionais específicas desempenham papel essencial.

